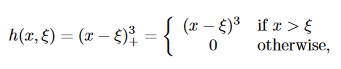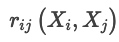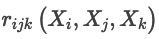广义相加模型（GAMs）

本文旨在根据自己的理解，对广义相加模型（GAMs）进行总结归纳，便于以后的回顾和查看。

概念

在现实生活中，变量的作用通常不是线性的，线性假设很可能不能满足实际需求，甚至直接违背实际情况，GAM是一种在线性的框架内，构造非线性的响应模型的方法。

GAM模型形式

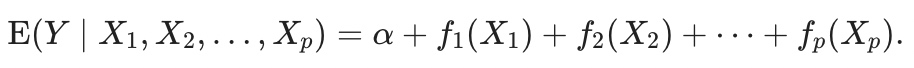
其中函数f可以是线性项、多项式项、样条函数或核函数。

样条函数

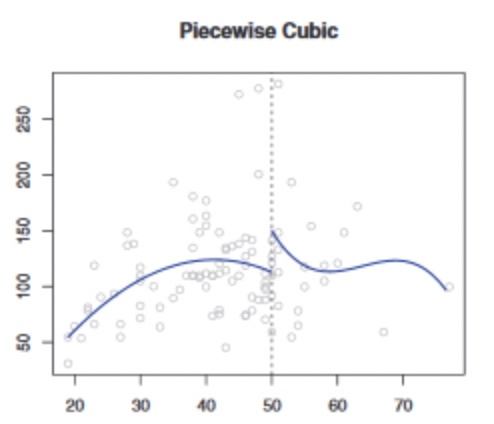
简单线性回归和多项式回归的拟合都是全局性的，使用相同的方程预测自变量的每一个值所对应的因变量。然而实际中随着自变量取值的变化，其与因变量之间的关系也可能是在不断变化的。

样条函数就是把自变量划分成多个连续的区间，每一个区间都用单独的线性函数或非线性的低阶多项式函数来拟合得到的函数。

节点数量的选取

可以使用广义交叉验证选择节点数。这种方法的基本思路是：

1. 取出一部分数据
2. 用某一数量的节点使样条拟合剩下的这些数据
3. 用样条拟合之前取出的数据
4. 重复步骤1-3，直到每个观察值都被取出过一次，计算整个交叉验证过程的均方根误差RMSE
5. 针对不同数量的节点重复1-4，最后选择最小RMSE时的节点数量

节点的位置

在数据变化复杂的地方多设置节点，在看起来更稳定的地方少设置节点。比如研究大气污染的健康效应时，在暴露反应关系可能存在拐点的地方设置节点。实际中，一般会截取长度相同的区间设置节点。

每个区间该如何确定拟合函数

理论上可以用任意低阶多项式拟合某个单独区间，最终得到的模型就是分段多项式。但分段多项式不能随便设定，它有两个限制条件：

• 连续性：多项式在节点处应该是连续的；
  
• 平滑性：相邻多项式的导数必须相同(如果拟合的是m阶多项式，则应保证相邻多项式的一阶导数至m-1阶导数均相等)；
  

常见样条函数：

• 三次样条函数：具有连续性、且一阶和二阶导连续的三阶分段多项式
  
• 薄板样条函数：可同时平滑多个变量，因此一般在研究多个变量的交互作用时使用

求解

假设我们样条函数为g(x),再求得该函数参数的同时，如何保证样条曲线的平滑性呢？
添加对平滑性的惩罚项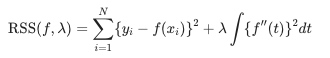

上式中的惩罚项表示为对区间t内，一阶导数g′(t)累计的变化情况，因此可以用来衡量该段区间整体的平滑性。
整体拟合函数项为：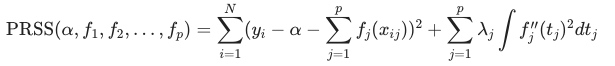

backfitting方法

使用backfitting（回修）方法求解整体拟合函数，方法流程为：

优缺点

1. 可以引入非线性函数;
2. 非线性可能使得对预测的更准确;
3. 因为是”加性的”，所以，线性模型的假设检验的方法仍然可以使用;
4. 因为是“加性”假设，所以GAMs中可能会缺失重要的交互作用，只能通过手动添加交互项来弥补，如下所示：
   
   

总结

可加模型提供一个有用的线性模型拓展，使得不仅保留着大部分的可解释性，也更加灵活；