uplift模型实践与应用
1. 背景
目前小流量实验存在的问题:
- 小流量实验结论负向和持平偏多,产品优化策略无法获得正反馈。
- 对照组和实验组流量都是随机划分,无法定位到真正受益人群。 核心解法思路:
- 根据用户画像、用户活跃度和用户行为特征,通过uplift增益模型对手百实验进行增益学习,发现对手百指标的影响(正向、负向、无影响),找到产品策略”敏感人群”;筛选出高增益的用户进行人群投放,提升手百关键指标,如DAU、留存等;
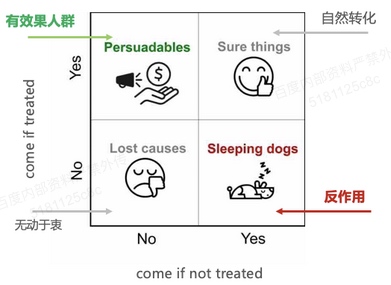
根据uplift模型,可将人群划分至下面四象限中,找到persuadables(实验带来正向效果)的人群,具体如下:
2. 理论综述
2.1 混淆变量
混淆变量是指在解释变量X和Y之间的因果关系时,存在的同时影响$X$和$Y$的变量$C$,如果不对其进行控制,会得出虚假的因果关系。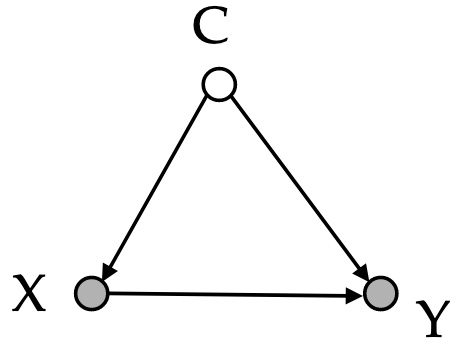
2.2 辛普森悖论
辛普森悖论(Simpson’s paradox)是概率统计中的一种现象:在混淆变量 Z 的每一个分层上,变量 X 和变量 Y 都表现出一致的相关性,但是在 Z 的整体上,X 和 Y 却呈现出与之相反的相关性。该现象于 20 世纪初就有人讨论,但一直到 1951 年 E.H.辛普森在他发表的论文中阐述此一现象后,该现象才算正式地被描述解释,辛普森悖论这个名字是由柯林·布莱斯(Colin R. Blyth)在 1972 年提出的。
2.2.1 神奇药物
以 BBG 药物(Bad/Bad/Good Drug)之谜为例,假设有一种新药 D,这种新药似乎可以降低心脏病发作的风险,我们通过临床观测收集到了如下数据(数据来自观测实验而非随机化实验):

整体来看,服药组和未服药组各有 60 人,男性和女性各有 60 人,不同人群的心脏发病率表现如下:
- 对于女性患者:未服药组的心脏病发病率 5% < 服药组的心脏病发病率 8%;
- 对于男性患者:未服药组的心脏病发病率 30% < 服药组的心脏病发病率 40%;
- 对于所有患者:未服药组的心脏病发病率 22% > 服药组的心脏病发病率 18%;
这种药物似乎对女性有害,对男性也有害,但却对整个人类有益!一个表面的解决方案是,当我们知道病人的性别是男性或者是女性时,我们不采用这种药物疗法,但如果病人的性别是未知的,我们就应该采用这种疗法!但显然,这个结论是荒谬的。这三句话中一定有一句是错的,但错的是哪一句?为什么?这种令人迷惑不解的情况究竟是如何发生的呢?
2.2.2 吸烟者存活率更高?
在 1995 年发表的一份关于甲状腺疾病的研究报告中,数据显示吸烟者的存活率(76%)比不吸烟者的存活率(69%)更高,寿命平均多出20年。然而,在样本的7个年龄组中,有6个年龄组中不吸烟者的存活率更高,而第7个年龄组中二者的差异微乎其微。年龄显然是吸烟和存活率的混杂因子:吸烟者的平均年龄比不吸烟者小(很可能是因为年老的吸烟者已经死了)。根据年龄来分割数据,我们就可以得出正确的结论:吸烟对存活率有负面影响。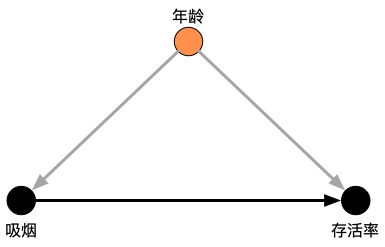
辛普森逆转通常满足两个前提:
- 不同$Z$ 分层对应的$Y$ 值相差很大:男性患者的发病率(33.3%)远高于女性患者的发病率(6.7%);
- $Z$在干预组和对照组的分布有明显差异:男性在对照组占比(66.7%)远高于在干预组占比(33.3%);
2.3 因果推断
2.3.1 因果定义
数据科学所研究的因果关系是经验世界中事件之间的因果关系,正如休谟所言,在经验世界中,我们实际所能观测到的只是事件本身,而无法观测到隐藏在事件背后的“因果机理”,事件间的因果关系本质上是对事件序列间特定关系的概括性称谓。
如果变量 A 和变量 B 满足以下三个条件,则称 A 和 B 之间存在因果关系“A 导致 B”,其中 A 被称为 B 原因,B 被称为 A 的结果:
- A在时间上必须先于 B;
- A和B应当在经验上相互关联;
- A和B之间观测到的经验相关不能被第三个导致 A 和 B 两者的变量所解释;
相关性只是因果性的一个必要非充分条件,即相关性不一定意味着因果性。
2.3.2 鲁宾因果推断模型
因果推断是研究变量间因果关系的学科,可以有两个方向:
- 考察结果的原因:看到结果,寻找结果背后的原因,这种研究往往是科学的起点,但寻找结果背后的原因,非常复杂。某一种结果产生的原因可能有很多,需要通过详细的调查、深入的分析才能找到。
- 考察原因的结果:主要关注某一干预对结果的影响,一项干预对结果变量产生的影响,通常称为因果效应(causal effects)或干预效应(treatment effects)。
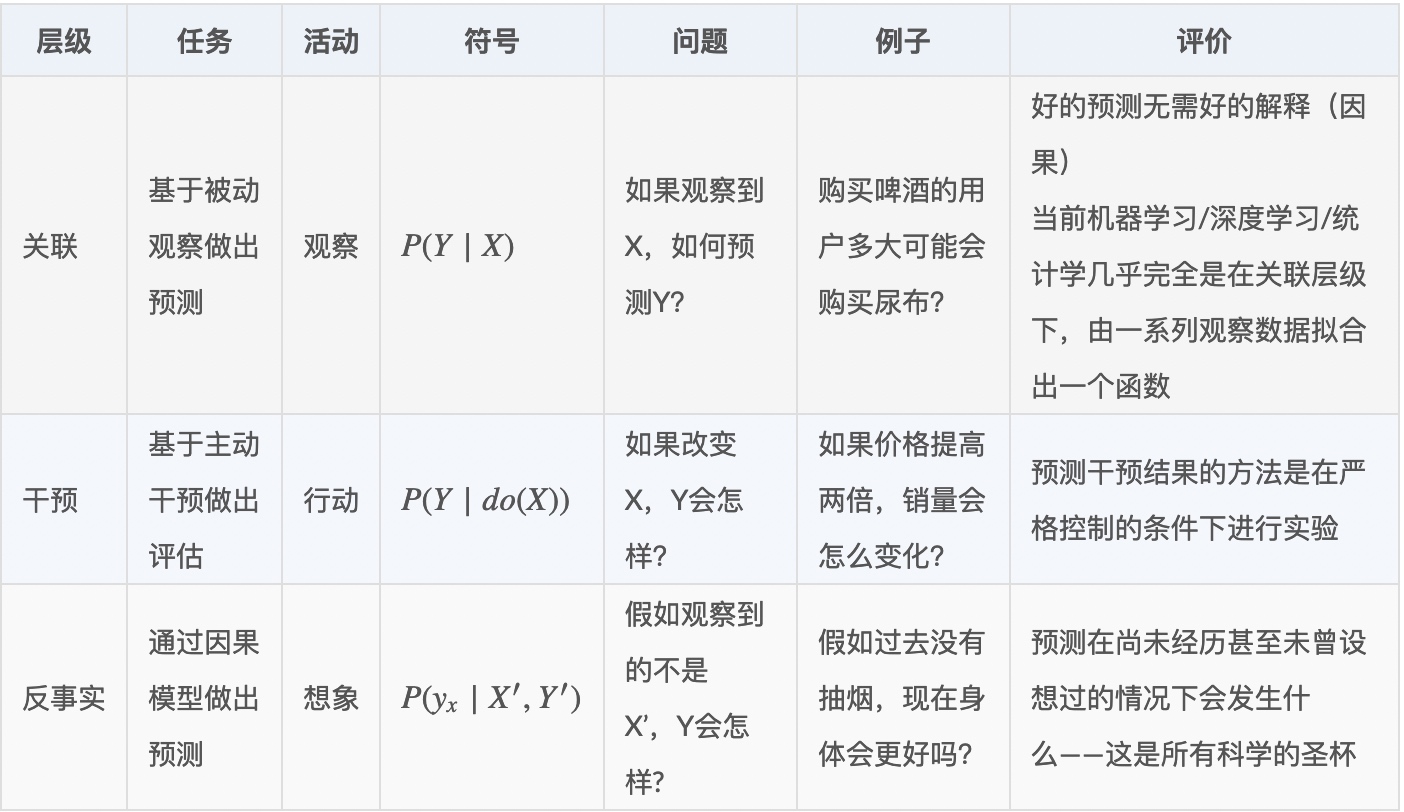
以上三种因果层级进行了详细描述,并将其称为”因果关系之梯“:
鲁宾因果模型(Rubin causal model, RCM)是一种基于潜在结果框架(framework of potential outcomes)的因果推断方法。RCM 有三个基本要素:潜在结果、稳定性假设、分配机制。
2.3.2.1 潜在结果
在因果推断中,必须有干预(Intervention),没有干预就没有因果(Rubin,1974)。干预可以是一项政策、一项措施或一项活动等,比如实施 4 万亿财政刺激方案,服用某种新药等。
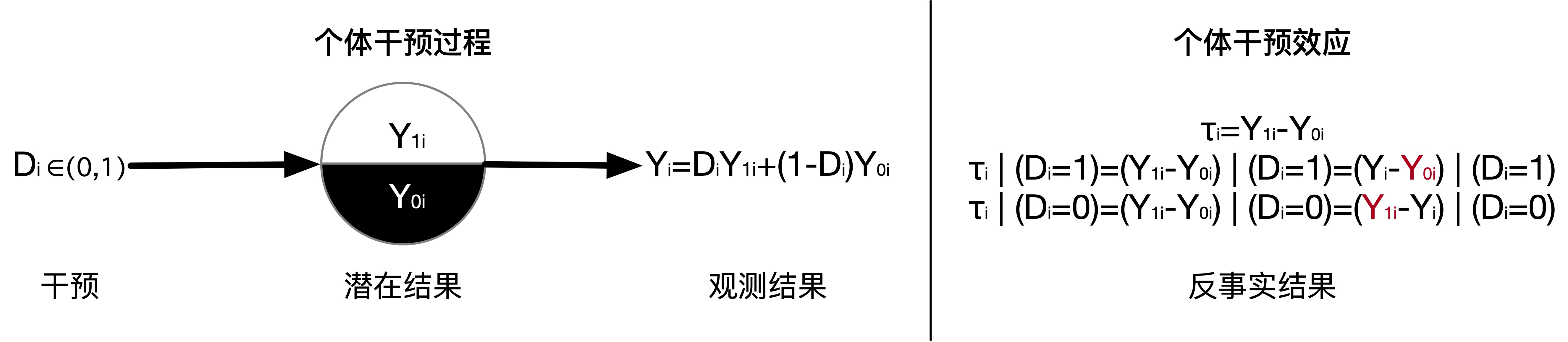
在干预状态实现之前,有几个干预状态就有几个潜在结果(Potential outcome),而干预状态实现之后,只有一个潜在结果是可以观测到的。
当干预状态实现之后,我们仅能观测到实现状态下的潜在结果,称为观测结果(Observation outcome),没有实现状态下的潜在结果是无法观测的,通常称为反事实结果(Counterfactual outcome)。
一个人不可能同时踏入两条河流,不可能同时处于两种状态,因而,观测研究中,不可能同时看到个体所有的潜在结果。无法同时观测到个体所有潜在结果的现象称为因果推断的基本问题(Holland,1986)。
观测结果 $Y_{i}$与潜在结果之间的关系,可以用下面的公式表示: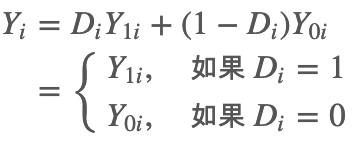
2.3.2.2 干预效应/因果效应
有了潜在结果的概念,个体因果效应的定义非常直观,不需要对分配机制进行任何内生性或外生性的假设,也不需要对结果变量的函数形式进行任何假设,对于个体$i$,某项干预的因果效应是两种状态下的潜在结果的比较:
$\tau_{i} = Y_{1i} -Y_{0i}$
因果效应的定义仅依赖于不同潜在结果的比较,对于给定个体,研究者只能观察到该个体一个状态下的潜在结果,因而,如果仅有一个个体,我们是没有办法得到个体因果效应的。因果推断的核心内容,实际上是想办法将未观测到的潜在结果估计出来,即反事实结果估计。估计反事实结果必须要用到多个个体,多个个体的选择方式有两种:
- 同一个体的不同时间:比如,判断一种药物是否对感冒有治疗效果,我们往往根据自己以往的经历。我以前感冒的时候吃药感冒就好了,我今天没吃药,头就很痛,因而,我们认为药物有治疗效果。其实这种推断中,我们进行了很强的假设,我们假设过去的经验可以作为今天吃药的反事实结果。如果这一假设不成立,我们就不能用过去吃药的结果作为今天吃药的反事实结果。因为今天的”我”与过去的”我”是不同的个体,我今天可能心情不好,不吃药头很痛,即使吃药,头仍然是痛的。这并不一定说明药没有治疗效果,而是因为我心情沮丧,使我的头更痛了,即我的头痛还混杂了其他的影响因素。
- 同一时间的不同个体:很多时候,我们的推断是利用同一时间不同个体的信息来估计反事实结果。比如考虑大学教育对收入的影响。在上大学之前,我们不确定大学能给我们带来什么。我们只知道目前我的结果是什么样子,或收入是什么水平。但不知道大学毕业之后收入会是什么水平。那我们在决定是否上大学时,是怎么作出决定的呢?我们可能会观察那些上了大学的人,可能是亲戚或朋友家的孩子,现在已经大学毕业了,有个很好的工作,获得比较满意的收入。那我们在作决策时是怎么做的呢?我们可能将他们的结果或收入作为我们上大学的潜在收入,从而决定是否上大学。
2.3.2.3 稳定性假设
RCM 的第二个要素是稳定个体干预值假(Stable Unit Treatment Value Assumption, SUTVA),简称稳定性假设(Rubin,1980),SUTVA 有两层含义:
- 不同个体的潜在结果之间不会交互影响:比如,我们住在同一间宿舍,我们两个都感冒了,如果药物对我头痛的治疗效果依赖于你有没有吃药,那就不满足稳定性假设;在社会科学中,没有交互影响的假设可能不成立,社会科学的研究对象往往是人的行为,个人行为之间往往存在交互影响;但是,在不存在交互影响的假设下,因果推断更加容易,通常假设不同个体之间不存在交互影响。
- 干预水平对所有个体都是相同的:比如考察药物的治疗效果,那么给所有病人的药物在药效上都应该是一样的,不能有的人有效成分是全额的,有的人是半额的;实际研究中,往往很难完全满足这一要求,通常会忽略掉这种差异,更加关注稳定性假设的第一项要求。
2.3.2.4 分配机制和条件独立性假设
分配机制是描述为什么有的人在干预组,有的人在控制组的机制。
条件独立性(Conditional independence Assumption),也称为非混杂性(Unconfoundedness)或者CIA假设,是指控制协变量 $X_{i} $后,个体干预状态的分配独立于潜在结果;通俗来说,就是进入干预状态的用户群的反事实结果与进入控制态的用户群的观察结果期望相等(就是后文提到的选择偏差=0),即去除混淆变量的影响。例如智力在研究教育和工资水平的因果关系时是混淆变量,因此在建立分配机制时,需要保证在同一智力下,去分配对照组和干预组计算因果效应,否则智力高的人更容易接受高等教育进入实验组,这些人即使不接受高等教育工资水平也比其他人高,无法得出教育对工资水平的因果效应。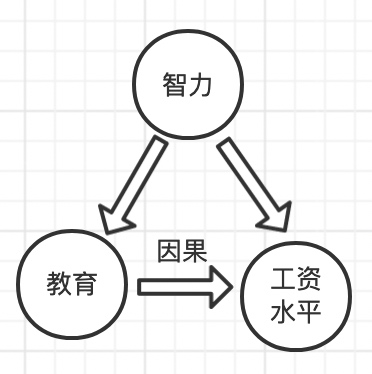
非混杂性可以表示为:
$\left ( Y_{1i},Y_{0i} \right )\perp D_{i}\mid X_{i}$
非混杂性在实际应用中可以分为两类:
- 实验研究:例如ab实验中,随机抽样就能保证非混杂性。
- 观测研究:需要人为设定分配规则,控制混淆变量(分层)影响,保证非混杂性。
几种概念的相关作用关系如下图所示: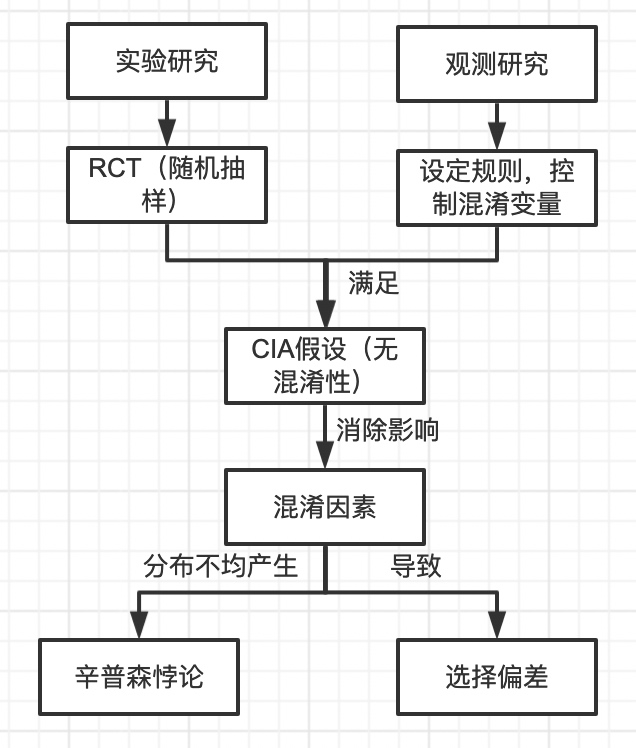
2.3.2.5 倾向性得分匹配(PSM)
在实验研究中,随机分配能很好的解决选择偏差的问题,但是在观测研究中,则没有办法通过随机来保证非混杂性,因此可以通过psm来解决这个问题。
理论上,如果我们对每一个实验组用户都在对照组里匹配一个得分相等(要求有点严苛)的用户,我们就能得到同质的实验组和对照组,就可以假装我们做了一个 A/B Test 了,接着就可以随意地进行组间比较了。
- 倾向性得分估算
这一步说白了,就是一个二分类建模问题。一般来说,按需做一下特征预处理,然后套一下LR模型就可以了。 - 倾向性得分匹配
假设我们已经有了每个用户的倾向性得分,我们的目标是针对目前的实验组用户,匹配得到一个近乎于同质的对照组。当用户量足够时候,一个简单做法是进行一对一无放回匹配:对于每一个实验组用户,我们去对照组里找一个倾向性得分最近的用户,把他们配成一对。匹配过程中,可以限制一下配对用户的得分差异不能超过某一个阈值,配不上就算了,以防把 “太不相似” 的用户匹配在一起。 - 因果效应推断
我们的目标是推断$ATT$ (Average Treatment Effect on the Treated)。
回顾一下,$ATT$ 的定义为 $𝐴𝑇𝑇=𝐸[𝑌_{1}−𝑌_{0}|𝑇=1]$。
现在我们已经有一对接近同质的实验组和对照组了,有很多方法可以用来估算 ATT 。
2.3.3 因果效应参数
2.3.3.1 ATE & ATT & ATC 定义
实证研究中,我们关心的往往不是某一特定个体的因果效应,而是干预的平均因果效应。假设有 $N$个个体,用 $i=1,……,N$ 表示,$Di∈0,1$ 表示干预变量,个体因果效应为:
$\tau_{i} = Y_{1i} -Y_{0i}$,$i=1,⋯,N$
个体因果效应往往无法估计,因此我们关注总体平均因果效应(Average Treatment Effect, ATE),它表示从总体中随机抽取一个个体进行干预的平均因果效应:
$τ_{ATE}=E[Y_{1i}−Y_{0i}]$
在政策评价中,我们更关心那些受到政策影响的个体的平均因果效应,称为干预组平均因果效应(Average Treatment Effect for the Treated,ATT):
$τ_{ATT}=E[Y_{1i}−Y_{0i}\mid D_{i}=1]$
有些时候,我们关注那些没有受到政策影响的个体如果接受政策干预的话,其平均因果效应是多少,称为控制组平均因果效应(Average Treatment Effect for the Control, ATC):
$τ_{ATC}=E[Y_{1i}−Y_{0i}\mid D_{i}=0]$
不同的因果效应参数回答不同的问题,比如考察大学教育对个体收入的影响,将大学教育看作一项积极干预,高中教育看作一项控制干预:
- ATE:如果想知道大学教育对所有国民的平均影响,估计的参数是总体的平均因果效应($ATE$),它反映的是如果全部国民均接受大学教育相对于均接受高中教育全部国民的平均收入增长。
- ATT:如果关心的政策问题是大学教育给接受者带来了多大程度的收入增加,需要估计的参数是干预组平均因果效应($ATT$)。
- ATC:如果想知道那些仅完成高中教育的个人,如果他们能够完成大学教育的话,他们的收入将增长多少,则需要估计的参数是控制组平均因果效应($ATC$)。
各个因果效应参数的定义如下所示: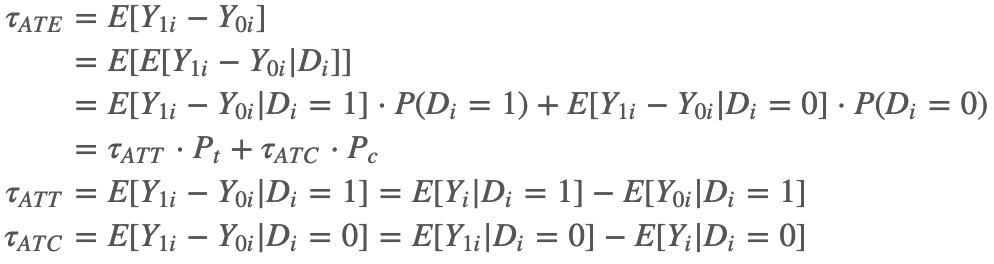
反事实结果 $E[Y_{0i}|D_i=1]和E[Y_{1i}|D_i=0]$ 是观测不到的,必须通过一定的方法将其估计出来,才能得到以上干预效应。
学过回归分析的学生可能禁不住想用 $Y_{i}$ 对 $D_{i}$回归,这也是计量经济学的基本建模方式,但是这种回归并不能识别出任何因果效应参数。比如我们建立一个简单的双变量回归模型:
$Y_{i}=\alpha +\tau D_{i}+\varepsilon _{i} $
根据初等计量经济学的知识,用一个容量为$N$的随机样本去估计上述简单回归模型,$D_{i}$的回归系数为: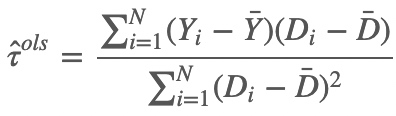
当干预变量是 0−1 二值变量时,可以证明 $Y_{i}$ 对 $D_{i}$ 的回归系数$\tau ^{\widehat{}ols} $等于干预组和控制组样本均值之差,在大样本的情况下: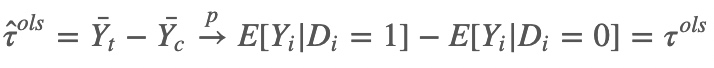
$\tau ^{ols}$是总体回归系数,一般不能反映因果效应参数,除非施加一定的假设。
首先,考察总体回归系数和干预组平均因果效应(ATT)之间的关系: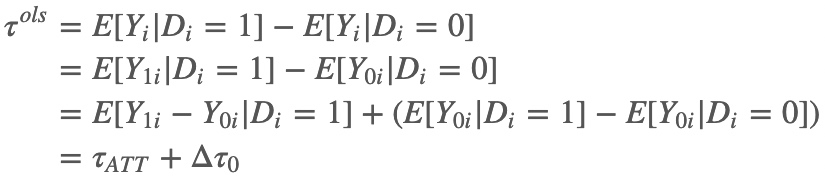
总体回归系数和对照组平均因果效应(ATC)之间的关系: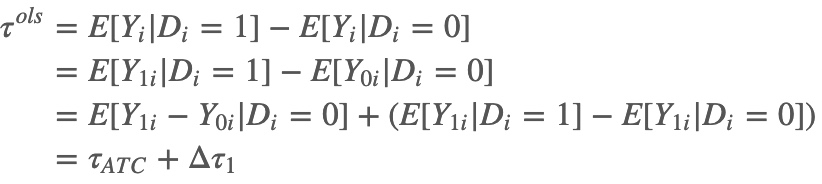
其中$\Delta \tau_{1} $和$\Delta \tau_{0} $,表示干预组和控制组个体在控制/对照状态下的潜在结果差异,也称为基线潜在结果差异(difference in baseline potential outcomes),这一偏差通常称为选择偏差。$E\left [ Y_{0i}\mid D_{i}=1 \right ] $和$E\left [ Y_{1i}\mid D_{i}=0 \right ]$表示干预组个体在控制状态下和控制组个体在干预状体下的潜在结果,是观测不到的,但是在选择偏差为0的假设下,可以用控制组的观测结果$E\left [ Y_{0i}\mid D_{i}=0 \right ]$来代替干预组的反事实结果$E\left [ Y_{0i}\mid D_{i}=1 \right ] $,用干预组的观测结果$E\left [ Y_{1i}\mid D_{i}=1 \right ]$来代替控制组的反事实结果$E\left [ Y_{1i}\mid D_{i}=0 \right ] $。
最后,总体回归系数通常也不是平均因果效应,只有同时施加假设$\Delta \tau_{1} =0$和$\Delta \tau_{0}=0 $,即选择偏差为0,总体回归系数才可解释为总体平均因果效应。在AB实验中,随机抽样很大程度解决了选择偏差和混淆变量(辛普森悖论)的问题。
将前面两个结论带入$\tau_{ATE} =P_{c} \cdot\tau_{ATC} +P_{t} \cdot\tau_{ATE} $
$\tau^{ols} =\tau_{ATE} +\triangle \tau_{0} +P_{c} \cdot \left ( \tau_{ATT}- \tau_{ATC} \right ) $
分配机制、潜在结果、干预效应和回归系数的转换关系如下图所示: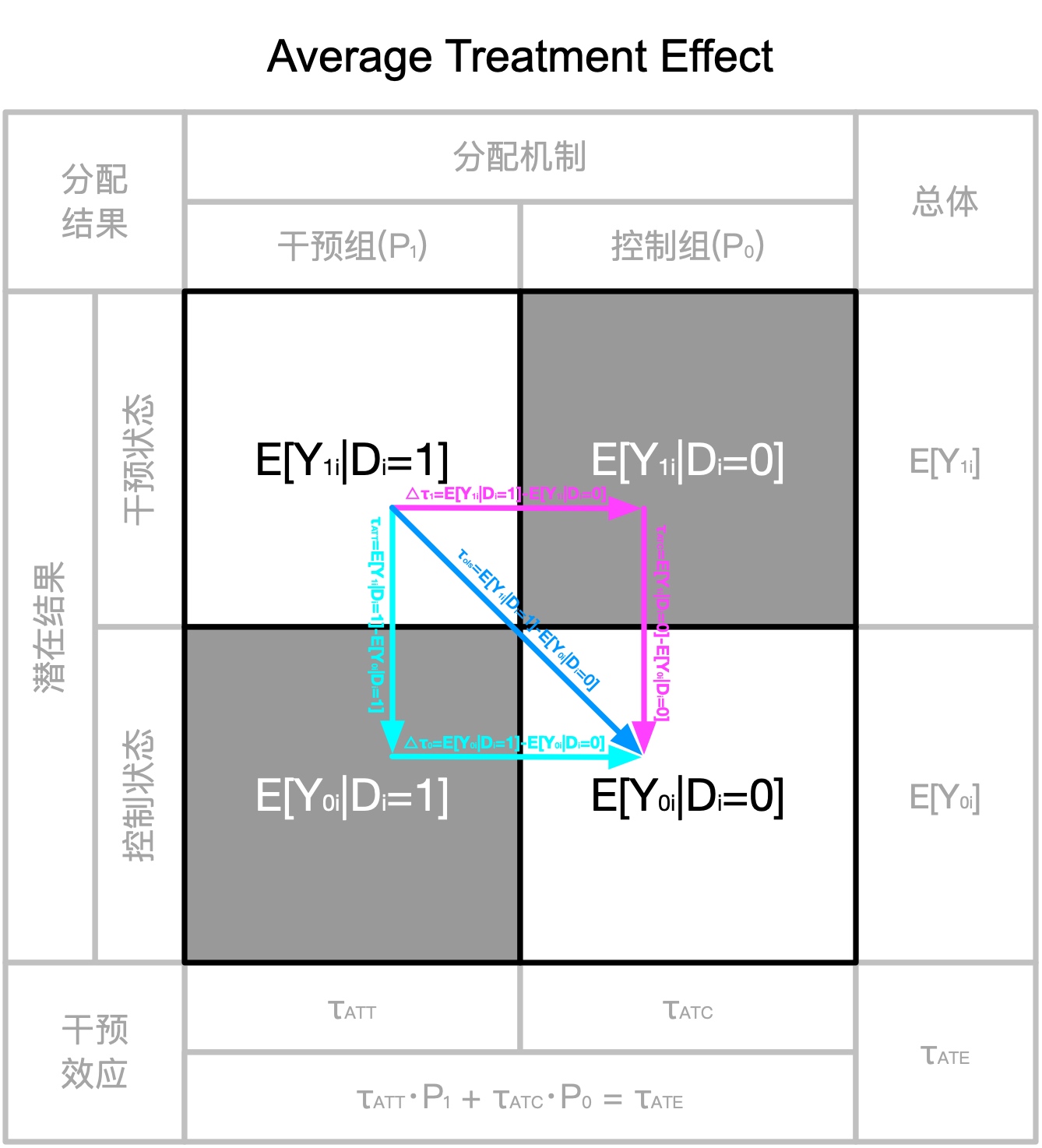
2.4 uplift模型
Uplift Models用于预测某种干预(treatment)对个体状态/行为的增量反馈价值(因果效应),也就是lift的部分:
$Lift = P\left (buy\mid treatment \right ) - P\left (buy\mid no \quad treatment \right )$
而传统模型通常直接预测目标:
$Outcome = P\left (buy\mid treatment \right )$
标签转换模型可以分为Meta Learner和Tree Learner两大类,其中Meta Learner包括标签转换模型/S_learner/T_learner/R_learner/X_learner等,Tree Learner包括回归树和分类树。
2.4.1 标签转化模型(Class Transformation Method)
标签转化模型适合二分类;
定义一个变量 $G ∈ \left \{ T , C \right \} $,$G=T$表示有干预,即实验组(treatment), $G = C$表示无干预,即对照组(control)。uplift分数$\tau$可以表示为: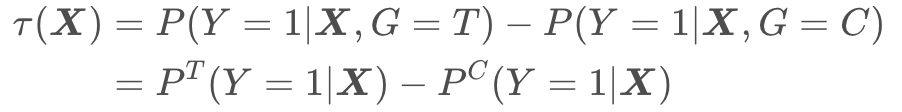
上式中 $ \boldsymbol{X}$ 表示用户特征, $P^T$表示用户在实验组中下单的概率(输出结果为positive), $P^C$ 表示用户在对照组中下单的概率(输出结果也为positive),uplift score就是两个概率的差值。
为了统一表示实验组和对照组都下单的情况( $Y = 1$),再定义一个变量 $Z$,$Z \in \lbrace 0, 1 \rbrace$: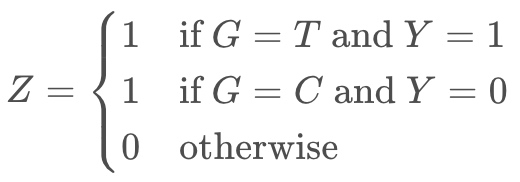
可以证明优化$\tau$等于优化 $P (Z=1 | \boldsymbol{X})$
假设干预策略 $G$与用户相互独立,即$G$独立于 $\boldsymbol{X} : P ( G ∣ X ) = P ( G )$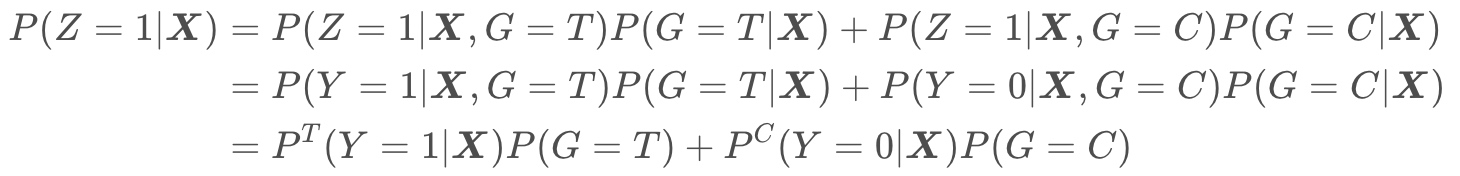
注意到$P(G=T)$和 $P ( G = C ) $是可以通过AB实验控制的,在随机化实验中,如果实验组和对照组的人数是相等的,那么 $P(G=T) = P(G=C) = \frac{1}{2}$,即一个用户被分在实验组(有干预策略)和被分在对照组(无干预策略)的概率是相等的。 在该假设下,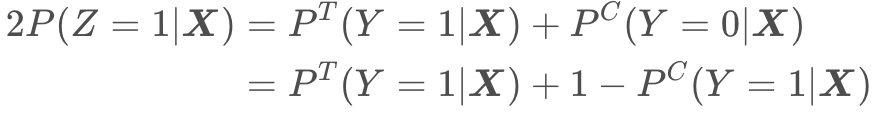
即: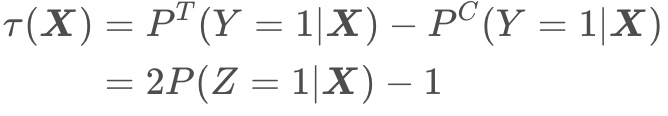
上式就是要计算的uplift score,此时只有 $Z$ 一个变量,可以直接对$Z=1$这建模,相当于优化$P(Z=1|\boldsymbol{X})$,而不需要分别对实验组($P^T$)和对照组($P^C$ )单独建模。而 $P(Z=1|\boldsymbol{X})$可以通过任何分类模型得到,所以这个方法称为Class Transformation Method. 实际上,$Z=1$就是实验组中下单的用户和对照组中未下单的用户,因此可以直接将实验组和对照组用户合并,使用一个模型建模,实现了数据层面和模型层面的打通。预测时,模型预测的结果就是uplift score.
标签转换需要满足两个假设:
- $G$与$X$相互独立,即用户特征与干预策略无关;
- $P(G=T) = P(G=C) = \frac{1}{2}$
2.4.2 S-learner(Meta-Learning)
把对照组和实验组放在一起建模,把实验分组$T$作为特征加入训练特征。如果该样本进入实验组vs对照组模型预测的差异作为对实验影响的估计。预测时将同一样本特征进行多次输入,每次只是改变不同的$T$值。一般而言,$T=0$ 表示对照组,$T = \left \{ 1,2,3\cdots \right \} $代表各个实验组。
计算步骤:
- 基于变量X和干预$T$训练预测模型;
- 分别估计干预和不干预时的得分,差值即为增量
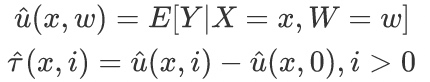
S-Learner模型训练时数据利用更充分,且建模更简单。
2.4.3 T-learner(Meta-Learning)
Two-Learner是基于双模型的差分模型,我们对实验组(有干预)和对照组(无干预)的购买行为进行分别建模,然后用训练所得两个模型分别对全量用户的购买行为进行预测,此时一个样本用户即可得出有干预和无干预情况下两个购买行为预测值。这两个预测值的差就是我们想要的uplift score。
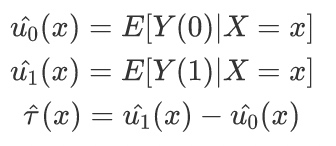
- 优点:简单直观,可以复用常见的机器学习模型(LR、Tree Model、NN)。
- 缺点:数据利用不充分,没有很好地拟合两个群体之间的差异(也即$lift$信号)且对模型误差容易被放大。假设单个模型准确率都是90%,那么最后预测lift的精度只有81%.
2.4.4 X-learner(Meta-Learning)
X-Learner是针对上述提到的问题对T-Learner和S-Learner进行了融合。步骤如下:
- 分别对对照组和实验组进行建模得到模型M1,M2和T-Learner一样
- 把对照组放进实验组模型预测,再把实验组放进对照组模型预测,预测值和实际值的差作为HTE的近似。这里和S-Learner的思路近似是imputation的做法。
- 实验组和对照组分别对上述target建模得到M3,M4,每个样本得到两个预测值然后加权,权重一般可选propensity score,随机实验中可以直接用进组用户数,流量相同的随机实验直接用0.5感觉也没啥问题。
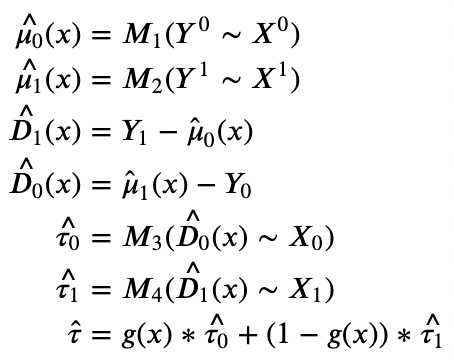
树模型(Tree-Based Method)
uplift树模型与机器学习中的CART树模型类似,同样分为回归树和分类树,区别在于机器学习中的分裂准则是基于信息增益,而uplift树模型是uplift score值。
分布散度可以度量两个概率分布之间的差异,因此我们可以将干预组和控制组理解为两个(关于Y的)概率分布,以此为分裂依据,若分裂后差异变大,则说明这个分裂有区分能力且有益于描述Treatment对Outcome的影响。常见的分布散度包括: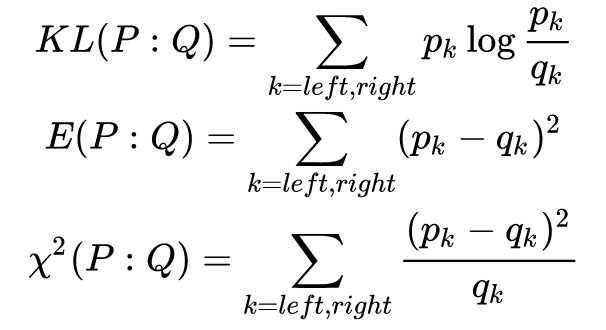
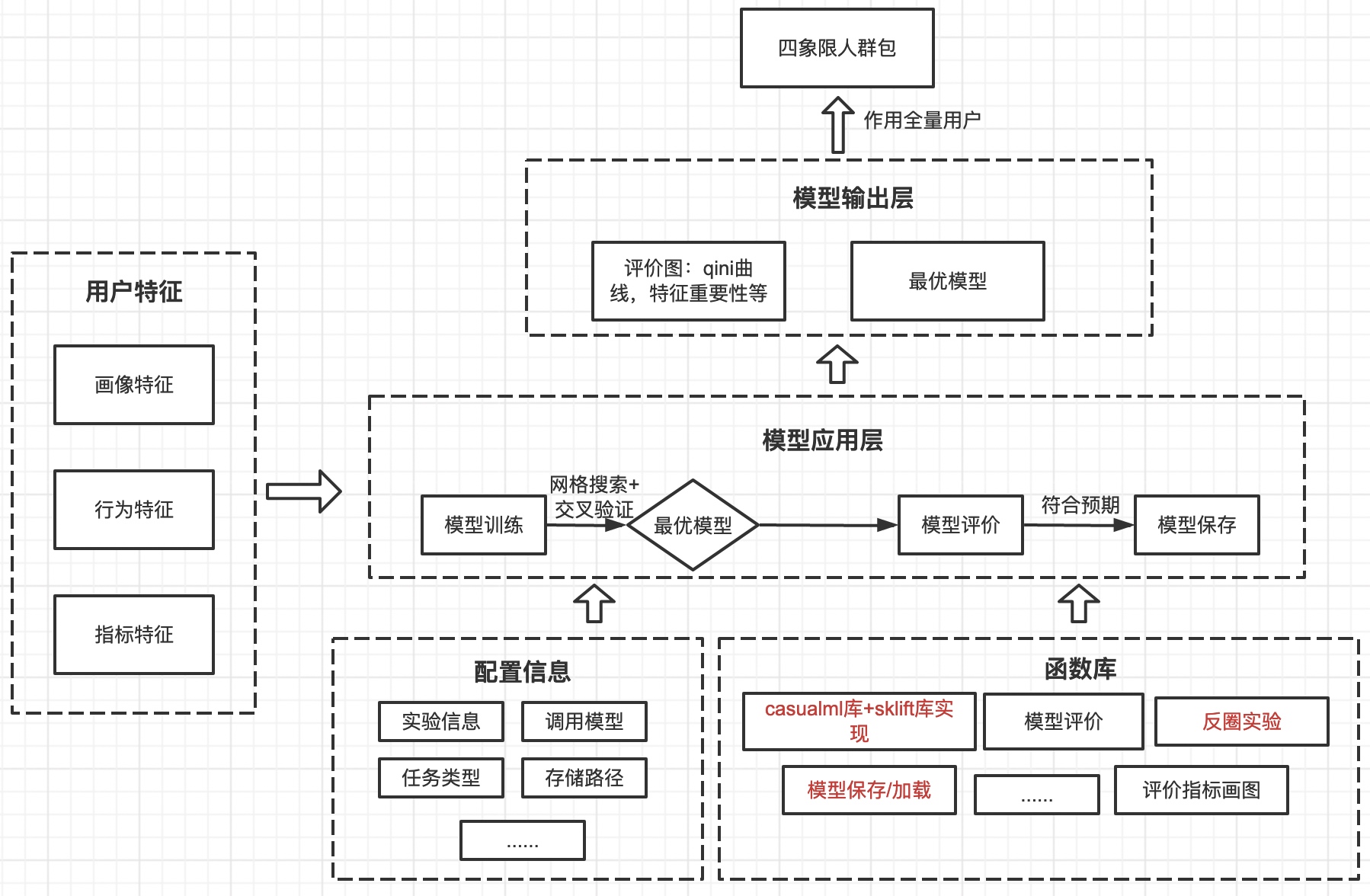
3. 整体框架
4.4 模型评价
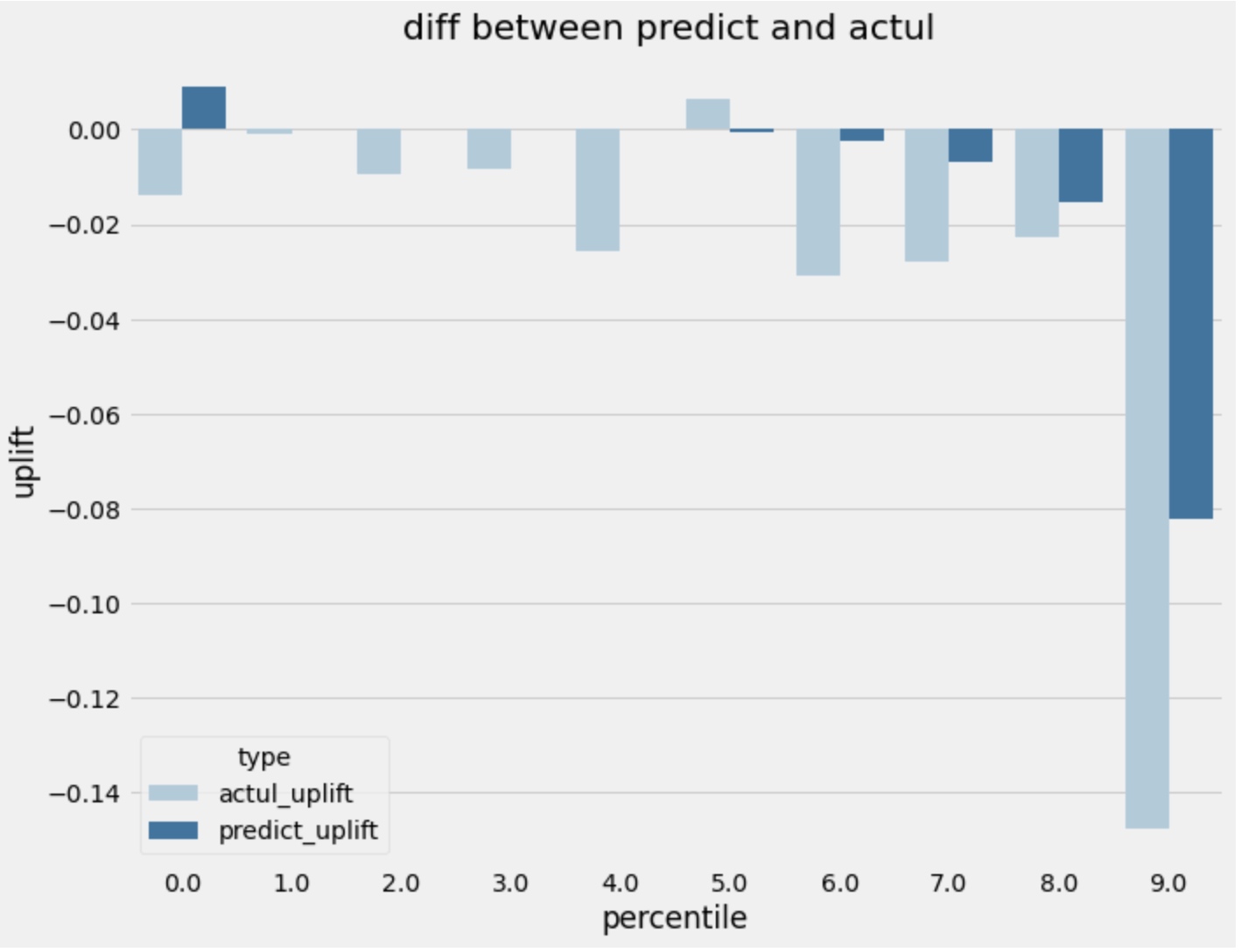
4.4.1 柱状图
将所有样本按照模型预测出的uplift score降序排列,按照等比氛围10组,通过比较组内的actual uplift score和预测pred uplift score的差异来评价效果。
- actual uplift score:组内实验组label均值-组内对照组label均值
- pred uplift score:足内预测uplift score均值
![-w709]()
评价原则:
- 单调性:actual和pred的uplift在单调行上是否一致,即是不是pred uplift越大的组,actual uplift同样越大,值越大,说明预测结果越有意义,结果区间为[-1,1]。例如:单调性为1,说明actual和pred之间呈现完全正向的函数相关关系,即actual uplift score是完全从高到低排列。
- 准确度:每个组内,actual uplift和pred uplift在数值上是否足够接近,值越大,说明准确度越高。例如准确度值为0,说明actual和pred之间uplift score完全相同,即预测结果达到完美。
- 区分度:就是最大的pred uplift(最左边那根柱子)和最小的pred uplift(最右那根竹子),差距足够大,值越大,说明模型区分度越大。例如:区分度为0,说明10组内predict uplift score都是同一个结果,这样一个没有区分度的模型实际上没有意义。
![806347bfce636834a2c803bed283d1a4]()
4.4.2 uplift score
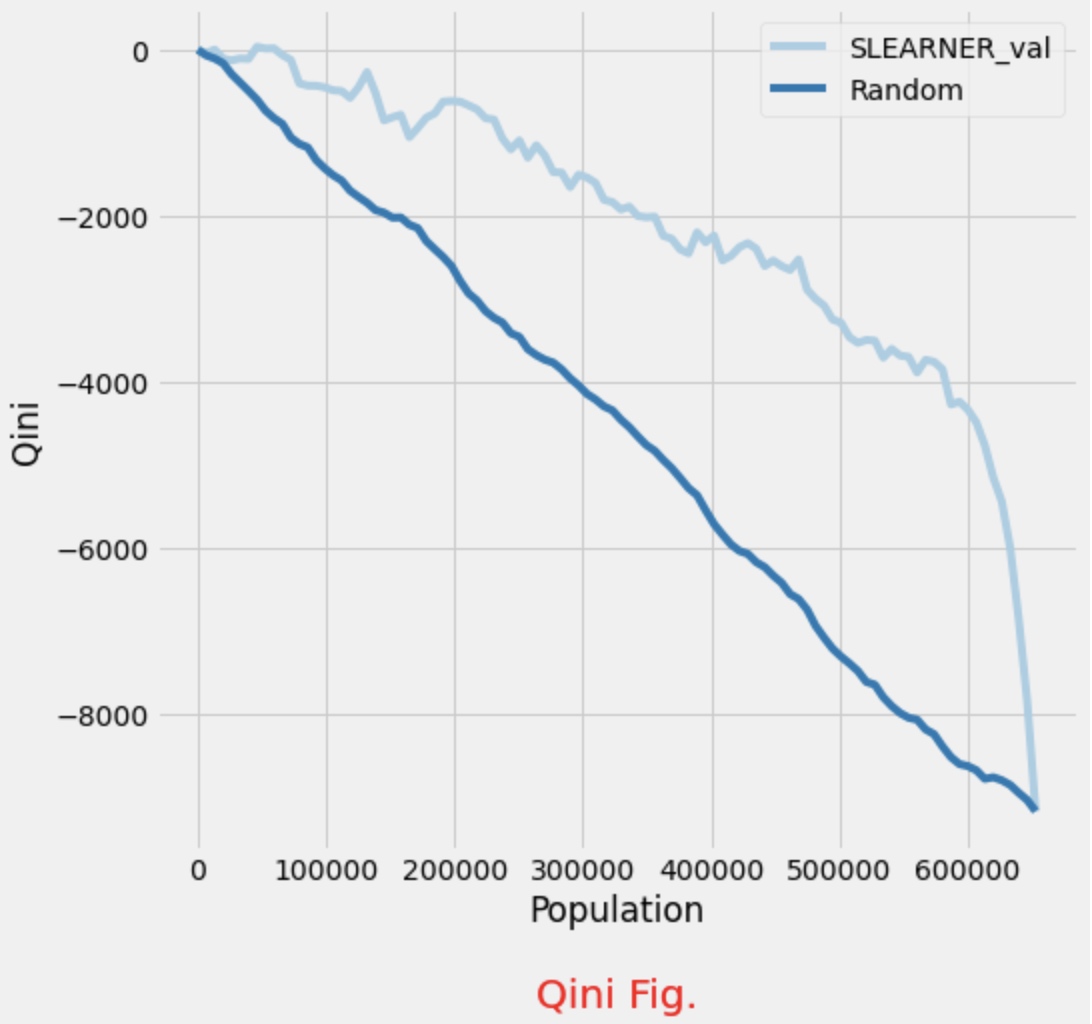
我们将数据集分组不断细分,精确到每个样本维度时,每次计算截止前t个样本的增量时,则得到Uplift Curve。公式如下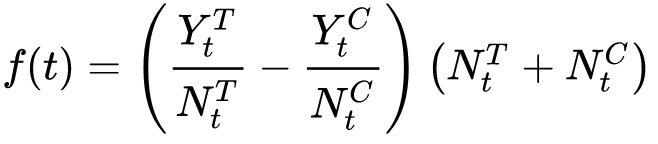
可视化如下,其中x轴为样本位序,y轴为累积增量数量。上方的每条曲线表示按照uplift score降序排列后,累积的增量效果;random直线表示随机排序(随机选择样本执行Treatment时)的增量效果;每条曲线终点相交,表示全量Treatment时的平均增量效果。
曲线中,越高拱的模型效果越好,数值化表示的话可以使用曲线下面积,与二分类评估中的AUC(Area Under ROC Curve)类似。这里称为AUUC(Area Under Uplift Curve),即 $\sum_{t}^{T} f\left ( t \right ) $。