检验方法与功效

我们做AB实验的时候，经常能看到这样一个指标：统计功效（power），或者是它的变体（）。
那么，这个所谓的统计功效到底是个啥呢？要理解功效，我们首先得理解两类统计错误。

1. 两类统计错误

假如我们做了一个AB实验，且两组用户的数据均值为和，我们会有两个初始假设：

：两个实验组之间的数据没有差别（），这个假设也叫”零假设”;
：两个实验组之间的数据存在差别（（）），这个假设也叫”非零假设”;

我们的假设有两种情况，对应的，真实结果页会有两种情况：

是对的：两组之间并没有真实差别;
是错的：两组之间存在真实差别;

我们把这2X2种情况进行交叉组合，就能看到4种结果：

显然，其中2.1和2.4都是我们预测正确的情况。而2.2和2.3则都是错误的，这两种错误，我们把它们分别予以表述：

2.2：实验本身没有效应，但我们觉得有效应。这是一类错误，或者叫错误
2.3：实验本身有效应，但是我们误以为没有。这是二类错误，或者叫错误

当我们人为设定了显著性水平后，就定了，一般为0.05，所以对应的统计量水平也就定了。第二类错误就是，即使没有达到拒绝的标准，但是其实是真的，我们却拒绝了它，这个错误的概率定义为，也就是犯二类错误的概率。

而统计功效，就是，即不犯二类错误的概率。换句话说，就是当AB两组差异真的存在时，我们能正确判断的概率。

根据其背后逻辑，我们可以知道，统计功效低，那么当AB两组差异真的存在时，我们很可能会错误判断两组差异不存在。换句话说，我们结果显示不显著，但其实真实情况是差异显著——我们错过了真实效应。这种情况，通常发生在我们的实验结果不显著时。

而更多的时候，我们觉得给我们带来实际困扰的会是一类错误。即AB两组其实没有差异，但我们误认为有差异。因此，以往的实验里，我们更多的会看到显著性水平。

最好是同时考虑和，把控制在一个合理的范围内。我们一般把统计功效定义在80%（或90%）以上，即在0.2（或0.1）以下。认为这样的可信度是可以接受的。

影响统计功效的因素有很多，主要的有3个：效应量、样本量和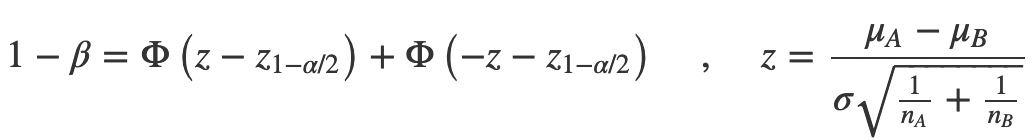水平。

1.1 效应量

两组间差异的效应量由以下公式定义：

• ：第一组的平均值
• ：第二组的平均值
• ：总体标准差

显然各组平均值的差值()越高，或标准差越低，都越容易检测到组间差异（有统计学意义的结果）。效应量越大，统计功效就越大。

1.2 样本量

显然，从整体中提取的样本越多，样本就越能代表整体，计算的效应量也越精确。但效应量是样本固有特性，样本量则是可以由自己掌握的，可以通过扩大样本量来提高实验的统计功效。

1.3 水平

水平也称显着性水平，即第一类错误概率，约定俗成地把它控制在0.05。如果把显着性水平降至0.01，实验能检测出差异的概率就更低了，也就是说，要是当p=0.03，我也只好说这两组没有统计学差异。

2. Cuped方法

在实际应用中，水平一般都是固定的，而流量基本都是固定且宝贵的，因此可以通过降低组间方差来提高统计功效。

CUPED的核心思路是构造了一个新的指标，假定实验原来观测的指标为，新的指标为（cv表示control variable），且将定义如下：

2.2 协变量特性

构造出来的有很好的特性，一是的均值是我们实验关注的指标Y的无偏估计，二是的方差小于原来指标的方差。如果能选取跟高度相关的协变量，那么的方差相比将会小很多。

2.1 协变量选取策略

其中是和的相关系数，也就是说如果能找到一个跟最相关的变量，那么的方差最小，从而方差缩减效果最明显。通常协变量可以使用指标空转期数据，一般选一周到两周就够了。协变量的数据不止可以用实验前数据，也可以用实验期间的数据，只要保证所选的协变量不会受实验策略的影响。比如用户首次进入实验的所属当天星期几就可以作为一个协变量。