EM算法

1. EM算法统计背景

EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation-Maximization Algorithm）。EM算法为了解决数据缺失情况下的参数估计问题。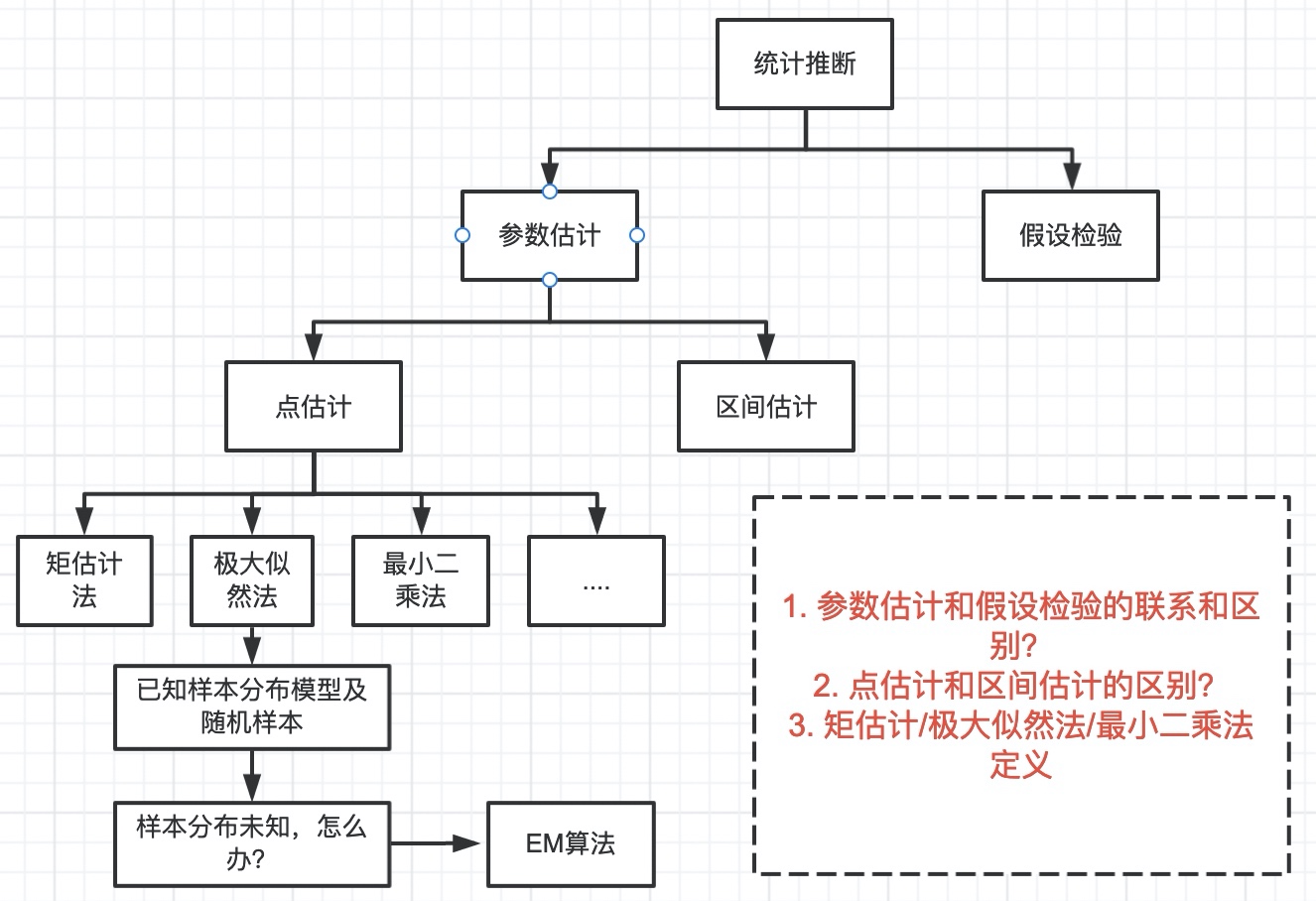

1.1 参数估计和假设检验

1.1.1 区别

• 参数估计是以样本资料估计总体参数的真值，而假设检验是以样本资料对总体的先验假设是否成立；
• 参数估计中的区间估计是以样本统计量为中心的双侧置信区间，假设检验既有单侧检验又有双侧检验；

1.1.2 联系

• 都是根据样本信息对总体的数量特征进行推断；
• 都是以抽样分布为理论依据，建立在概率论基础之上的统计推断；

1.2 点估计和区间估计的区别

点估计就是用样本统计量的某个取值直接作为总体参数的估计值；区间估计是在点估计的基础上，给出总体参数估计的一个估计区间，该区间通常由样本统计量加减估计误差组成，真实值在这个区间中的概率，就称之为置信水平（用1-α来表示，表示显著性水平），整个区间便称为置信区间。

点估计相比于区间估计的不足：由于样本是随机的，抽出一个具体的样本得到的估计值可能不同于总体真值，也无法说明点估计值的可靠性以及与总体参数的接近程度，因此需要对总体参数进行区间估计。

1.3 点估计方法

1.3.1 矩估计

用样本矩估计总体矩，从而得到总体分布中参数的一种估计。它的思想实质是用样本的经验分布和样本矩去替换总体的分布和总体矩。设有样本 ，而k为自然数，则样本矩做如下定义：

其中是阶样本原点矩，是阶样本中心矩。通过推导可知：

即样本的一阶原点矩是总体均值的无偏估计，样本的二阶中心矩是总体方差的有偏估计，统计量是总体方差的无偏估计。

• 优点是：简单易行, 并不需要事先知道总体是什么分布。
• 缺点是：当总体类型已知时，没有充分利用分布提供的信息。一般场合下，矩估计量不具有唯一性。

顺带介绍下评价估计量的标准：

• 无偏性(unbiasedness)：估计量抽样分布的数学期望等于被估计的总体参数；
• 有效性 (efficiency)：对同一总体参数的两个无偏点估计量，有更小标准差的估计量更有效；
• 一致性 (consistency)：随着样本量的增大，估计量的值越来越接近被估计的总体参数；

1.3.2 极大似然法

思想是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本（独立同分布）结果出现的模型参数值；具体是利用样本分布密度构造似然函数，然后对参数进行求导来得到参数的最大似然估计。

注意：当总体分布为正态分布时，有一个有趣的性质：通过极大似然法构建的模型的参数（均值和方差）直接就是样本矩（一阶样本原点矩和二阶样本中心距）

1.3.3 最小二乘法

主要用于线性统计模型中的参数估计问题。最小二乘法是一种数学优化技术，它通过最小化误差的平方和找到一组数据的最佳函数匹配。在线性回归中，若误差服从正态分布，则最小二乘法就是极大似然估计！

2. EM算法引入

首先引入一个经典例子来说明，假设我们现在想调查一个学校男女学生身高分布情况，首先随机抽取出了100个学生，每个学生的身高随机变量已知，并且知道男生和女生分别服从同一分布（假设是正态分布，其他分布也行），但是这个分布的均值 和方差 是未知的，这两个参数就是我们需要估计的。那么存在两种情况：

• 对于这100个学生，性别是已知的。
• 对于这100个学生，性别是未知的。

第一种情况：性别已知，很简单，根据是男是女可以知道其属于哪个分布（男生分布或女生分布），根据正态分布的概率密度函数构造出极大似然函数，然后求导，就可以求出两个分布相应的参数（均值 和方差 ）。正态分布的概率密度函数为：

第二种情况：性别未知，也就是说抓过来一个学生，我们都不知道其是男是女（呵呵，还真有可能布吉岛），EM算法就是用来求解这种情况的！

下面正式介绍EM算法：

2.1 由原问题构造出极大似然函数

在这个例子中，随机变量身高X是已知的，X就是观测变量，性别是未知的（但是客观存在，只是我们不知道罢了），就是隐变量。

对于一个包含m个样本的集合，假设隐变量 服从某未知分布，那么构造出的极大似然模型为：

理论上，对上述极大似然函数针对每个参数求偏导就可以，然而式子中包含和的对数形式，按照李航《统计学习方法》中所说，是没有解析解的。需要通过迭代的方法求解，首先通过jensen不等式进行处理。

2.2 jensen不等式处理似然函数

jensen不等式：假设是一个随机变量，是一个凸函数（一元：二阶导大于等于0，多元：海塞矩阵半正定），则：

如果二阶导大于零（海塞矩阵正定），是严格不等式，当是常量时，取等号；凹函数不等式方向取反。
凸函数如下所示：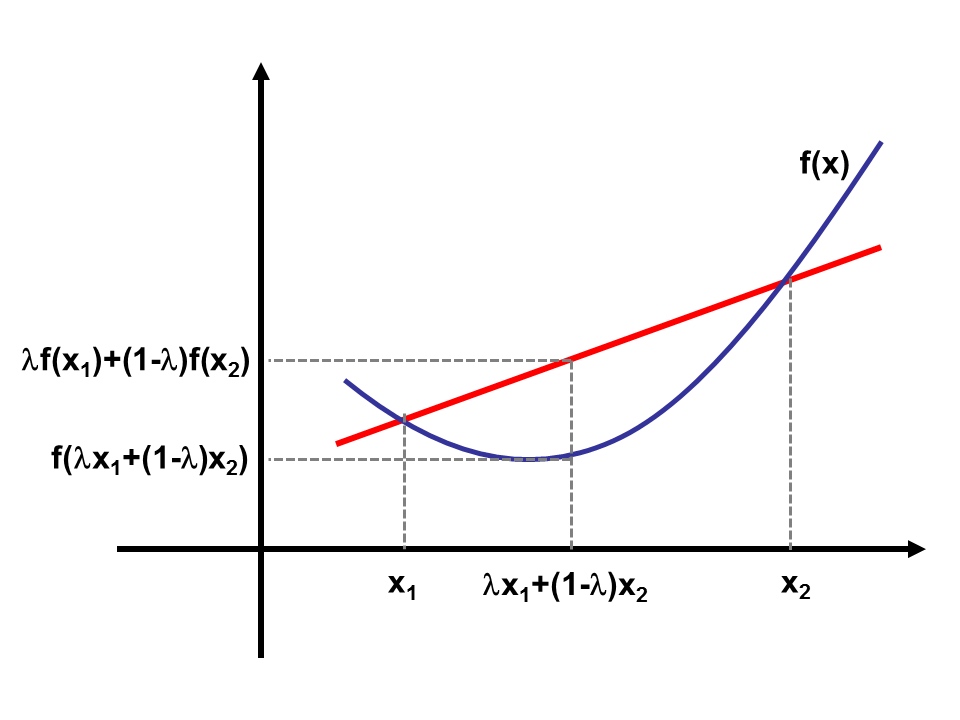

根据jensen不等式，对原极大似然函数进行变换：

其中。因为是凹函数，相当于是变量的期望（因为当是离散变量时，，是的函数，则，所以就可以得到公式（3）的不等式了），根据jensen不等式即可得到上述变形。上述变换将和的对数转换成了对数的和，偏导可以求解出来了，但是现在存在问题是：能不能将最大化转化为最大化（3）式？答案是能，但是如果需要满足一定条件？（关于如何推导出这个条件网上例子很多，并不难，想了解可以参考文末链接2），下面对该条件进行介绍。

2.3 转换条件

其实就是要使式（3）是的紧下界，即至少有点使（3）式中号成立，由jensen不等式知，当为常量，即变量等于一个常数constant时：

再根据条件，可以得到：

最终等于：

就是隐变量的概率分布（第个样本属于的概率）。

2.4 EM算法

也就是说我们需要根据模型参数求出隐变量的分布（即第个样本属于哪一个模型），然后带入（3）式极大似然函数中求解。。。。矛盾就出来了：求需要已知，求需要已知，对于开头举的例子来说就是：想要估计学生身高分布模型（混合高斯）的参数，我们需要先知道每个人是男是女，而想要知道性别又要先知道每个人所服从的分布。想要“鸡”需要先有“蛋”，想要“蛋”需要先有“鸡”，怎么办呢？

2.4.1 EM算法思想

先随机初始参数打破僵局，继而求出隐变量的分布，代入（3）式计算，得到一个更优的参数。。。这样不断更新参数，达到最终一个收敛值（是可以收敛的，这里就不证明了，有兴趣可以看下《统计学习方法》，里面有详细的证明）。

2.4.2 EM算法步骤

• E步：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，即隐性变量的期望。作为隐藏变量的现估计值：

• F步：根据极大似然函数（3）式，求得新的模型参数：

2.4.3 EM算法实例

下面通过通过抛硬币的例子来具体说明极大似然估计（下图a）和EM算法（下图b）的流程。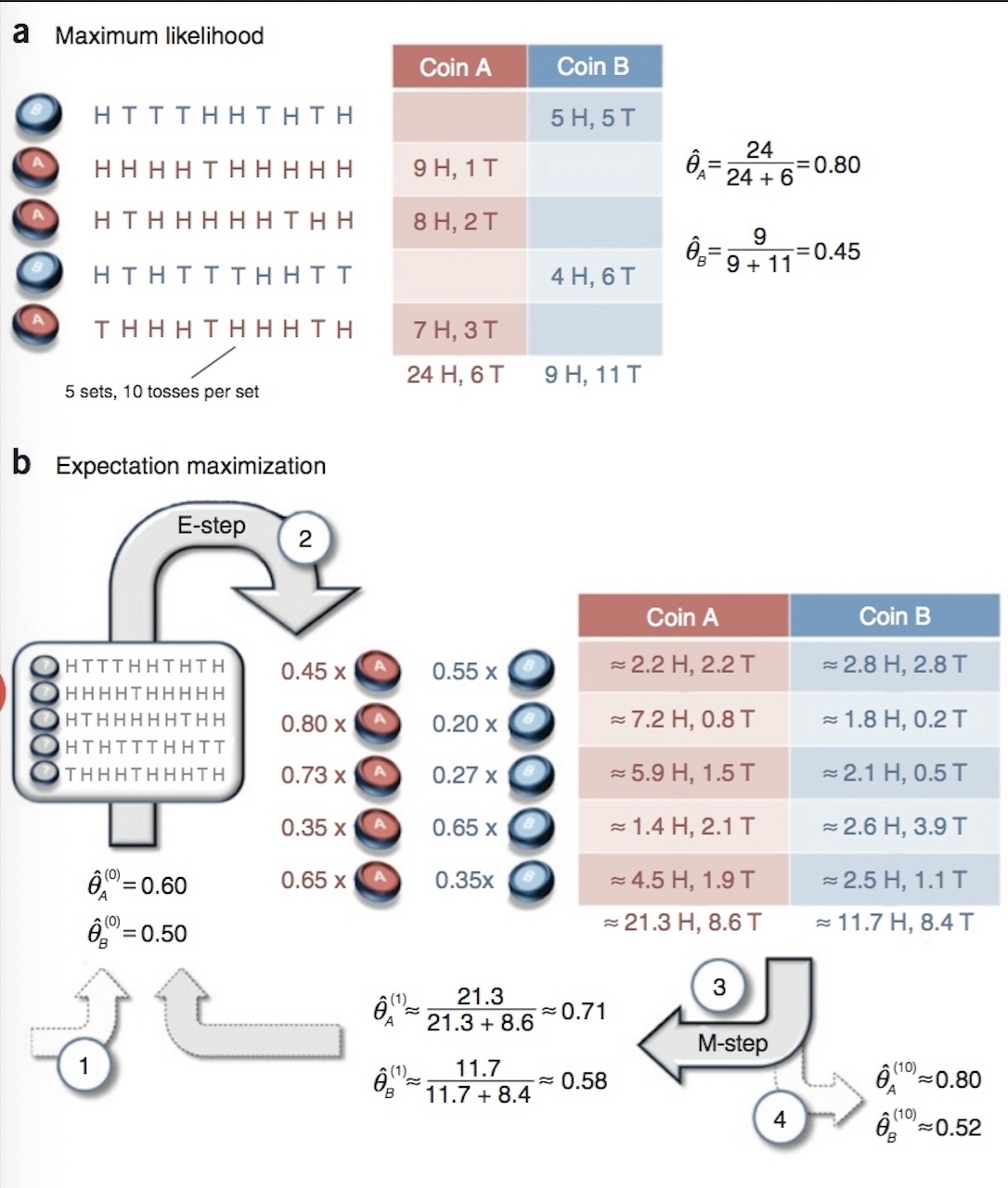

3. 后记

EM算法一般用于非监督学习中，常见的应用如求解高斯混合模型，另外k-means聚类算法中也用到了EM算法的思想：（1）

• E步：想要聚类，需要先知道有哪几类，因此先初始化k个点作为类中心。
• F步：根据得到的中心，对每个样本归类，然后更新得到新的类中心。

从这里我们也可以看出聚类和分类的联系，聚类时虽然不知道样本的类别，但是过程中隐含的假设并用到了样本的类别，分类则是直接告诉了样本类别。

4. 参考

《统计学习方法》 ——李航
（1）https://www.cnblogs.com/yymn/p/4769736.html
（2）http://blog.csdn.net/zouxy09/article/details/8537620
（3）https://www.cnblogs.com/txg198955/p/4097543.html