中心极限定理

1.中心极限定理

1.1 定义

中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。

其中注意两点：

1.2 总体本身的分布不要求正态分布

中心极限定理对总体的分布形式没有要求。例如我们掷一个骰子，其分布类型是是平均分布，但是最后每组的平均值也会组成一个正态分布。

1.3 样本每组要足够大，但也不需要太大

有一个大家疑惑的地方，样本容量足够大，多大才是足够大？这个问题的答案和总体分布的形状相关，如果样本本是来自近似对称分布的总体，那么当样本量取相当小（如样本量取5）的值的时候，正态逼近的结果也会非常好。然后，如果总体的分布严重倾斜，则样本量必须取相当大的值。根据检验，对于大多数总体来说，样本容量取30或者更大，就足以得到令人满意的正态逼近结果。

不同分布

卡方分布

若个随机变量是相互独立，符合标准正态分布的随机变量，则随机变量的平方和:

被称为服从自由度为的卡方分布，记作:

卡方分布重要定理：

分布

根据中心极限定理，只要样本量足够大，统计量的抽样分布（如样本均值）将遵循正态分布。因此，当我们知道总体的标准偏差时，我们可以计算统计量，并使用正态分布来评估样本均值的概率。

但是样本量有时很小，并且我们通常不知道总体的标准偏差。当这些问题中的任何一个出现时，统计学家依赖统计量（也称为分数）的分布，定义：

假设服从标准正态分布，服从卡方分布，那么的分布称为自由度为的分布,记为:

两点分布

随机变量只取两个值和，则称随机变量服从两点分布，或者分布。
且的期望为：

的方差为：

二项分布

二项分布是个独立的成功/失败试验中成功的次数的离散概率分布，其中每次试验的成功概率为。这样的单次成功/失败试验又称为伯努利试验;如果随机变量服从参数为和的二项分布，我们记为，且的期望为：

的方差为：

2.区间估计

2.1 单总体的参数检验

2.1.1 总体均值估计

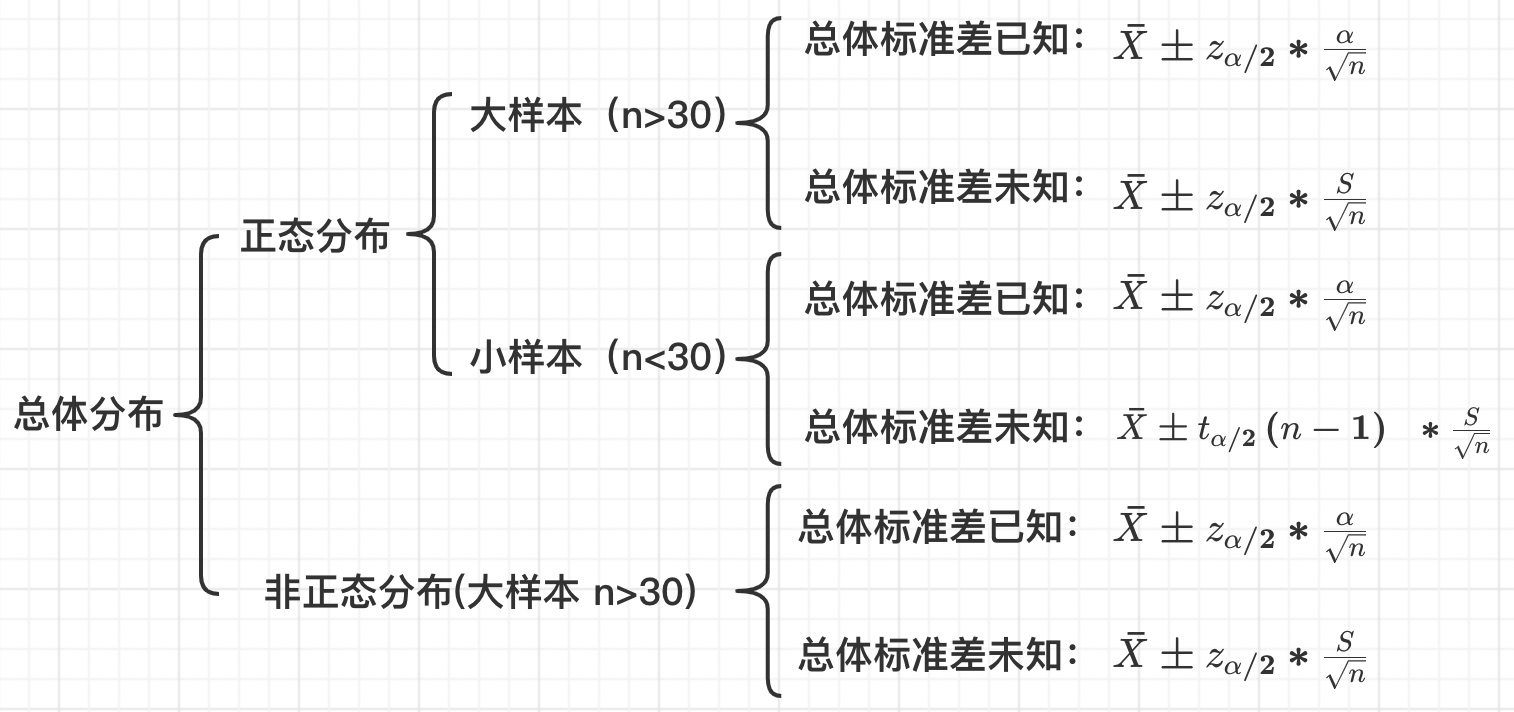
2.1.2 总体比例估计

总体比例只考虑大样本的情况：

2.1.3 总体方差估计

只考虑正态总体方差的估计。
因为：

所以可得总体方差的置信区间为：

2.2 双总体的参数检验

2.2.1 总体均值估计

2.2.2 总体比例估计

2.2.3 总体方差估计

3. 例子：如何用总体比例估计确定产品质量

3.1 背景

公司生产了一批产品，但这批产品到底怎么样，是不是所有的产品都符合质量标准，这批产品里有没有次品，产品的次品率又是多少，次品率是否符合国家标准？

在统计学中，我们把这批产品叫做总体，随机抽出的产品叫样本，而产品的品质可以用随机变量表示，的取值有两种可能：次品、非次品。此时若样本为次品的概率是,随机变量就服从一个两点分布，用表示，取值的概率情况即：

两点分布的期望（总体均值），方差。

我们称上述从总体中随机抽出一个样本的过程为一次伯努利实验，重复抽取次就是次伯努利实验。次抽样抽到次品的次数我们用另一个随机变量表示，的取值可能是，的分布即二项分布。

两点分布就是n=1的二项分布。

3.2 大样本区间估计

当产品的品质X服从两点分布时，两点分布具有一个显著特点总体均值等于，总体方差。样本量足够大时，总体比例的估计与大样本、方差未知时的总体均值估计类似，只是此时我们不再用样本方差代替总体方差（总体方差由组成）。

根据中心极限定理，样本量足够大时，样本均值渐进正态分布，而

可见样本均值的期望为,标准化的样本均值服从标准正态分布，可以构造统计量：

确定一类错误率（即置信度）,则有：

然后就可以得到次品率的取值范围。